10n คือ 10 หรือ 100 หรือ 1,000 ... ตัวเลขเหล่านี้ถ้านำไปเป็นตัวหาร จะได้ผลหารเป็นตัวเลขชุดเดียวกับตัวตั้ง แต่ตำแหน่งทศนิยมถูกเลื่อนไปทางซ้าย เท่ากับจำนวนเลข 0 ของตัวหาร เช่น
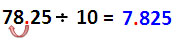 | หารด้วย 10 ตัวหารมีเลข 0 หนึ่งตัว ได้ผลหารเป็นเลขชุดเดียวกับตัวตั้งแต่ตำแหน่งทศนิยมถูกเลื่อนไปทางซ้าย 1 ตำแหน่ง |
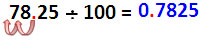 | หารด้วย 100 ตัวหารมีเลข 0 สองตัว ได้ผลหารเป็นเลขชุดเดียวกับตัวตั้งแต่ตำแหน่งทศนิยมถูกเลื่อนไปทางซ้าย 2 ตำแหน่ง |
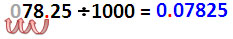 | หารด้วย 1,000 ตัวหารมีเลข 0 สามตัว ได้ผลหารเป็นเลขชุดเดียวกับตัวตั้งแต่ตำแหน่งทศนิยมถูกเลื่อนไปทางซ้าย 3 ตำแหน่ง ถ้าจำนวนหลักของตัวตั้งไม่พอให้เติม 0 |
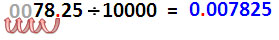 | หารด้วย 10,000 ตัวหารมีเลข 0 สี่ตัว ได้ผลหารเป็นเลขชุดเดียวกับตัวตั้งแต่ตำแหน่งทศนิยมถูกเลื่อนไปทางซ้าย 4 ตำแหน่ง ถ้าจำนวนหลักของตัวตั้งไม่พอให้เติม 0 |
เนื่องจากการหารด้วยตัวเลขในกลุ่ม 10n นั้นหาผลหารได้ง่าย เราจึงพยายามแปลงตัวหารให้เข้ามาอยู่ในกลุ่ม 10n โดยอาศัยคุณสมบัติที่ว่า เมื่อคูณตัวตั้งและตัวหารด้วยเลขคงที่ตัวเดียวกัน ผลหารจะไม่เปลี่ยนแปลง
ตัวอย่างที่ 1
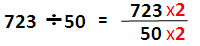 | ตัวหารเป็น 50 สามารถแปลงให้เป็น 100 โดยคูณด้วย 2 ถ้าคูณ 2 ที่ตัวหาร ต้องคูณ 2 ที่ตัวตั้งด้วยเพื่อให้ผลหารไม่เปลี่ยนแปลง |
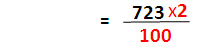 | ตัวหารกลายเป็น 100 ทำให้หาผลหารได้ง่าย |
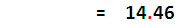 | 723 x 2 = 1446 เมื่อหารด้วย 100 จะได้ผลหารเป็นเลขชุดนี้ แต่ตำแหน่งทศนิยมถูกเลื่อนไปทางซ้าย 2 ตำแหน่ง |
ตัวอย่างที่ 2
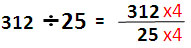 | ตัวหารคือ 25 สามารถแปลงให้เป็น 100 โดยคูณด้วย 4 ต้องคูณทั้งตัวตั้งและตัวหารเพื่อให้ผลหารไม่เปลี่ยนแปลง |
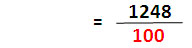 | นำ 4 ไปคูณ 312 หาคำตอบได้ง่ายกว่า นำ 25 ไปหาร 312 |
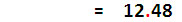 | คำตอบของการหารด้วย 100 คือใส่ทศนิยม 2 ตำแหน่ง |
แม้ว่าจะไม่สามารถแปลงตัวหารให้อยู่ในรูป 10n แต่ถ้าสามารถแปลงให้ตัวท้ายเป็น 0 ก็ได้ประโยชน์จากคุณสมบัติของ 10n เพราะถ้าตัวท้ายเป็น 0 แสดงว่ามี 10 เป็นตัวประกอบ
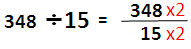 | นำ 2 ไปคูณ 15 เพื่อแปลงตัวหารให้ลงท้ายด้วย 0 เนื่องจาก 15 x 2 = 30 |
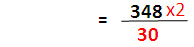 | เมื่อคูณ 2 ที่ตัวหารแล้ว ต้องคูณ 2 ที่ตัวตั้งด้วยเพื่อให้ผลหารไม่เปลี่ยนแปลง |
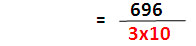 | นำ 30 มาแยกตัวประกอบจะได้ 3 x 10 |
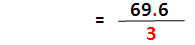 | นำ 10 ไปหาร 696 ได้ 69.6 |
 | นำ 3 ไปหาร 69.6 ได้ผลหารคือ 23.2 |
เนื่องจากการหารด้วย 10 นั้นหาคำตอบง่ายกว่าหารด้วย 9 เราจึงนำคำตอบของการหารด้วย 10 มาใช้เป็นค่าประมาณของคำตอบของการหารด้วย 9 เพราะ 9 มีค่าใกล้กับ 10
เทคนิคการหารด้วย 9
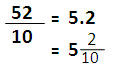 | ถ้าหารด้วย 10 เศษจากการหารคือตัวเลขหลักสุดท้ายของตัวตั้ง |
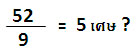 | ถ้าหารด้วย 10 ได้ผลหารคือ 5 ดังนั้นคำตอบของการหารด้วย 9 ต้องไม่ต่ำกว่า 5 เพราะตัวหารมีค่าน้อยลง ผลหารจะมีค่ามากขึ้น หารด้วย 10 เหลือเศษ 2 ถ้าหารด้วย 9 ต้องได้เศษมากกว่า 2 คำถามคือ ได้เศษเท่าไร |
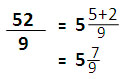 | 9 มีค่าน้อยกว่า 10 อยู่ 1 ถ้าใช้ 9 แทน 10 ในการหาร จะได้เศษเพิ่มขึ้นอีก 1 สำหรับแต่ละครั้งที่หาร นำ 10 ไปหาร 52 ได้ 5 ครั้ง ถ้านำ 9 ไปแทน 10 และหาร 52 ได้ 5 ครั้งจะเหลือเศษเพิ่มขึ้น 5 X 1 = 5 หารด้วย 10 เหลือเศษ 2 หารด้วย 9 เหลือเศษเพิ่มขึ้นอีก 5 ดังนั้นเศษจากการหารด้วย 9 คือ 5+2 |
เทคนิคการหารด้วย 9
เพื่อให้ง่ายในการนำหลักการนี้ไปใช้กับโจทย์ข้ออื่น เราสรุปขั้นตอนการหารด้วย 9 ดังนี้
| 1. | เปลี่ยนตัวหารจาก 9 เป็น 10 เพื่อประมาณผลหารเบื้องต้น นำผลหารของ 10 ที่เป็นจำนวนเต็มมาเป็นค่าประมาณผลหารของ 9 |
| 2. | แบ่งตัวตั้งเป็นเลข 2 จำนวน จำนวนแรกคือหลักหน่วย ส่วนที่เหลือคือจำนวนที่สอง |
| 3. | เศษที่ได้จากการหารด้วย 9 คือผลบวกของเลข 2 จำนวนที่ได้จากการแบ่งในขั้นที่ 2 |
| 4. | ถ้าเศษที่ได้มากกว่า 9 (ตัวหาร) แสดงว่าผลหารที่ประมาณไว้ในขั้นที่ 1 ต่ำกว่าความเป็นจริง ให้นำ 9 ไปหารเศษ แล้วนำผลหารไปบวก กับผลหารที่ประมาณไว้ในขั้นที่ 1 (หารด้วย 9 คือทำซ้ำขั้นตอนที่ 1 - 4 อีกรอบ) |
ตัวอย่างต่อไปเป็นการนำหลักการที่สรุปไว้ 4 ขั้นตอนนี้ไปใช้
ตัวอย่างที่ 1
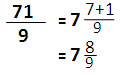 |
|
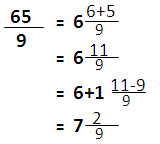 |
|
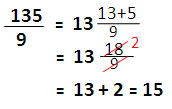 |
|
ตัวอย่างที่ 4
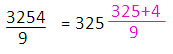 |
|
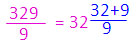 |
|
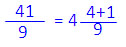 |
|
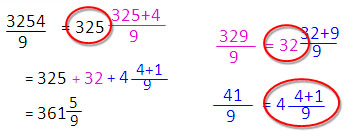 | คำตอบสุดท้ายคือนำผลหารที่ประมาณไว้ทั้งหมดมารวมกันคือ 325 + 32 + 4 = 361 เศษจากการหารคือเศษในขั้นตอนสุดท้าย แม้ว่าตัวอย่างนี้ จะพิสูจน์ว่าขั้นตอน 4 ขั้นตอนที่กำหนดไว้สามารถใช้ได้เสมอ ไม่ว่าตัวตั้งจะเป็นเลขกี่หลัก แต่ไม่แนะนำให้ใช้วิธีนี้กับโจทย์ที่ตัวตั้งมากกว่า 3 หลัก เพราะต้องวนทำซ้ำ 4 ขั้นตอนหลายรอบ ทำให้ได้คำตอบช้ากว่านำ 9 ไปหารโดยตรง เทคนิคการหารโดยแยกตัวประกอบ เทคนิคนี้เหมาะกับโจทย์ที่ตัวหารเป็นเลข 2 หลักหรือมากกว่า 2 หลัก ให้นำตัวหารมาแยกตัวประกอบเพื่อลดขนาดของตัวหารให้เล็กลงเป็นเลขหลักเดียว จึงหารได้ง่าย และลดความเสี่ยงในการคิดเลขผิด เพราะจำนวนเลขมีขนาดเล็กลง ตัวอย่างที่ 1
ตัวอย่างที่ 2 กรณีที่หารไม่ลงตัว สามารถเลือกตอบเป็นเลขทศนิยมหรือเลขเศษส่วน ตัวอย่างนี้แสดงการหาผลหารโดยวิธีแยกตัวประกอบ และตอบเป็นเลขทศนิยม (หารไม่ลงตัว)
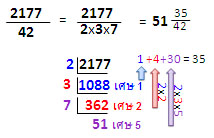
ตัวอย่างที่ 3 แสดงการหาผลหารโดยวิธีแยกตัวประกอบ และตอบเป็นเลขเศษส่วน (หารไม่ลงตัว)
|
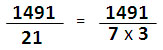
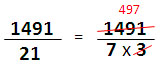
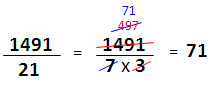
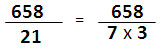
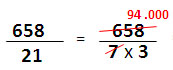


ไม่มีความคิดเห็น:
แสดงความคิดเห็น